TL;DR
本来今天计划把面向对象设计原则剩下的几条原则写一写的,结果一大早看了架构师训练营的本周作业题:用你熟悉的编程语言实现一致性hash算法,并编写测试用例测试这个算法,测试100万KV数据,10个服务器节点的情况下,计算数据分布数量的标准差,评估算法的存储负载不均衡性。
正好前阵子读协议的时候读过一致性哈希算法,正好,就着这个题目,可以深入的研究并实践一下了,于是,按耐不住内心的躁动,暂且先写这篇吧。
以下是本文的大纲:
- 什么是一致性哈希
- 解决了什么问题
- 动手实现一致性哈希
以下是正文开始。
0x01 什么是一致性哈希
维基百科上的定义:一致性哈希其实就是一种特殊的哈希算法。在使用一致哈希算法后,哈希表槽位数大小的改变平均只需要对$K/n$个关键字重新映射,其中$K$是关键字的数量,$n$是槽位的数量。然而在传统的哈希表中,添加或删除一个槽位几乎需要对所有关键字进行重新映射。
这里的槽位你可以把它简单的想象成数组中的一个位置。
上面的定义提到了传统的哈希表,也就是我们平时使用哈希的场景。比如,平常我们的哈希算法都是对服务器节点的数量或者是目标对象的数量之类的数值进行取模来计算哈希值,如下图所示:
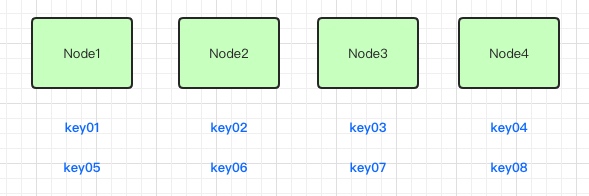
我们这里假定了有四台服务器,八个key值去映射取模,结果会均匀的分布到四台服务器的节点上。当我们增加一台服务器时,如下图示:
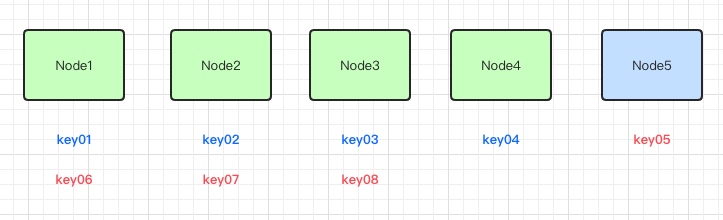
因为节点的总数量发生了变化,所以会导致大量的key通过哈希函数取模的结果发生变化。同样,当有服务器发生故障下线时:
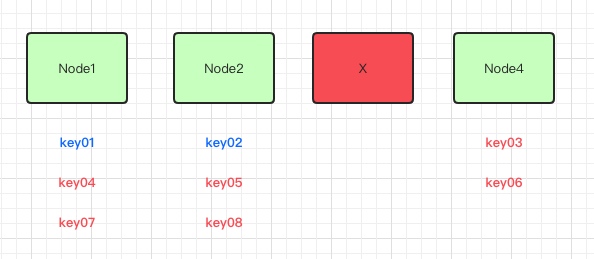
同样的道理,也会导致大量的key通过哈希函数取模的结果发生变化。
这个哈希函数对key的计算结果(也就是哈希值)发生了变化会导致怎样的影响呢?
如果是在分布式缓存的场景下,大量的哈希值取模的结果变化直接会导致大量缓存无法命中(因为同样的的键被映射到了不同的服务器上,而缓存的值还在原来的服务器上),直接穿透到DB;同时原来缓存的值还在内存中,所以会浪费很多内存。
如果是在负载均衡的场景下(假如是以用户ID为key),大量的哈希值取模的结果变化直接会导致大量用户新的请求会落到和之前不同的服务器上,如果正好你的应用会在服务器本地保存一些用户状态相关的数据的话,此时大量用户请求在新的服务器上,新的服务器又需要重新去获取或是计算来得到这些用户数据。(不过现在大多数情况下都会做无状态化设计,个别特殊的功能除外)
无论是上面哪一种情况,结果都是不可接受的,因为在分布式场景下,服务的节点上线下线太平常不过了。一致性哈希就可以一定程序上来解决这些问题。
0x02 解决了什么问题
一致性哈希是对$2^{32}$进行取模来计算哈希值的。准确的说,一致性哈希的值范围是$[0,2^{32}-1)$,每一个值可以理解为是一个槽位(slot)。
取模操作会使这里计算的哈希值形成一个环(哈希值到达右边界之后,下一个值又会从左边界处的值开始,图形化表示时就类似一个环形),所以我们也把这种哈希算法称为哈希环。
哈希环的空间是按顺时针方向组织的,我们可以通过计算哈希算法的值来将节点映射到哈希环上:
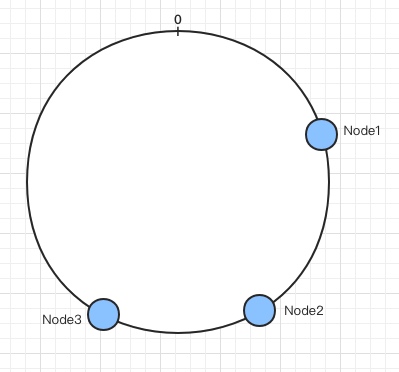
上图就把三个节点(用蓝色小圆圈表示)映射到了哈希环上,当需要对某个指定的key读写的时候,一般分为两步来操作:
- 第一步会将
key作为参数通过哈希函数来计算哈希值,以此来确定这个key在哈希环上的位置; - 第二步是从这个计算出来的位置以顺时针方向沿哈希环行走,遇到的第一个节点就是
key对应的节点;
如下图所示:
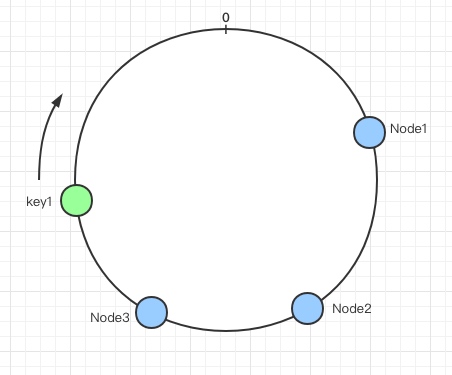
从上面,我们可以看到,确定一个key在哈希环的位置是通过哈希函数来计算的,所以这个哈希函数就是一致性哈希的核心。
还有一种情况,有时候,我们的节点数量比较少的时候,通过哈希函数将节点映射到哈希环上之后,当有大量的key进行哈希时,可能会出现大部分的哈希值通过哈希环所计算出来的节点比较集中在某个节点上,为了解决这个问题,有人就引入了虚拟节点的概念:
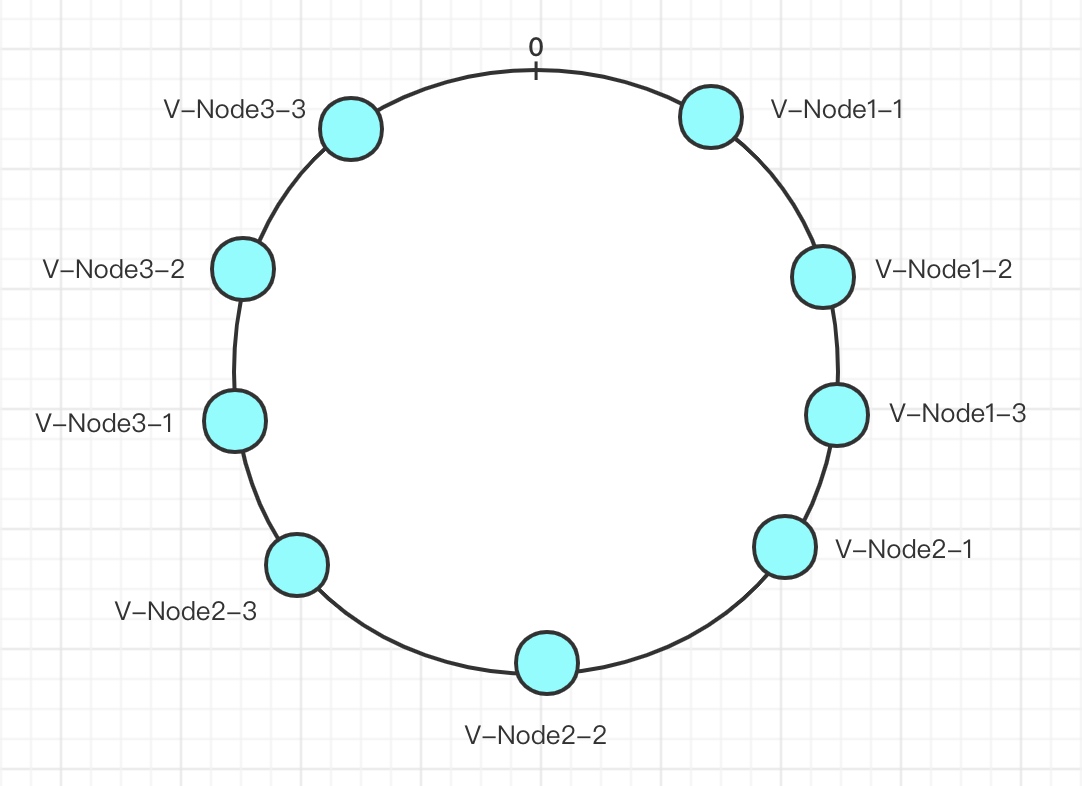
如上图所示,我们将前面第一张图中的三个节点,分别给每个节点映射成三个虚拟节点,这样,整个哈希环上就有了九个节点,相比较三个节点而言,九个节点(尽管最终还是映射到三个真实的节点)会让整个分布变得更加的均匀(均匀是相对的)。(还有一种做法是将真实的节点和虚拟节点一起映射到哈希环上)
另外,前面讲到了传统哈希方式在分布式环境下的会带来大量数据迁移的问题,那一致性哈希如果解决这个问题呢?这一点维基百科中已经说明了:
当删除一台节点机器时,这台机器上保存的所有对象都要移动到下一台机器。添加一台机器到圆环边上某个点时,这个点的下一台机器需要将这个节点前对应的对象移动到新机器上。 更改对象在节点机器上的分布可以通过调整节点机器的位置来实现。
可以看到,无论是节点上线还是下线,只需要移动极小的一部分数据即可,尤其是与传统的哈希方式相比,一致性哈希带来的收益是非常可观的。
对于哈希函数,我们需要关注哪些呢?
我们用哈希函数来对key求值,然后到哈希环上所查找映射的节点,所以我们需要哈希值的均匀程度;再者,哈希算法本身会有一个哈希碰撞的问题,这个碰撞率当然是越低越好;最后就是关注性能了,根据不同的使用场景,优先考虑需求的情况下再考虑较好的性能,不同哈希算法的算法复杂度也不一样。
关于哈希函数的算法实现,根据不同的使用场景,维基百科上列出了几十种。
0x03 动手实现一致性哈希
现在来解决本篇开头的那道题。
在Guava中的哈希函数的实现列表如下:
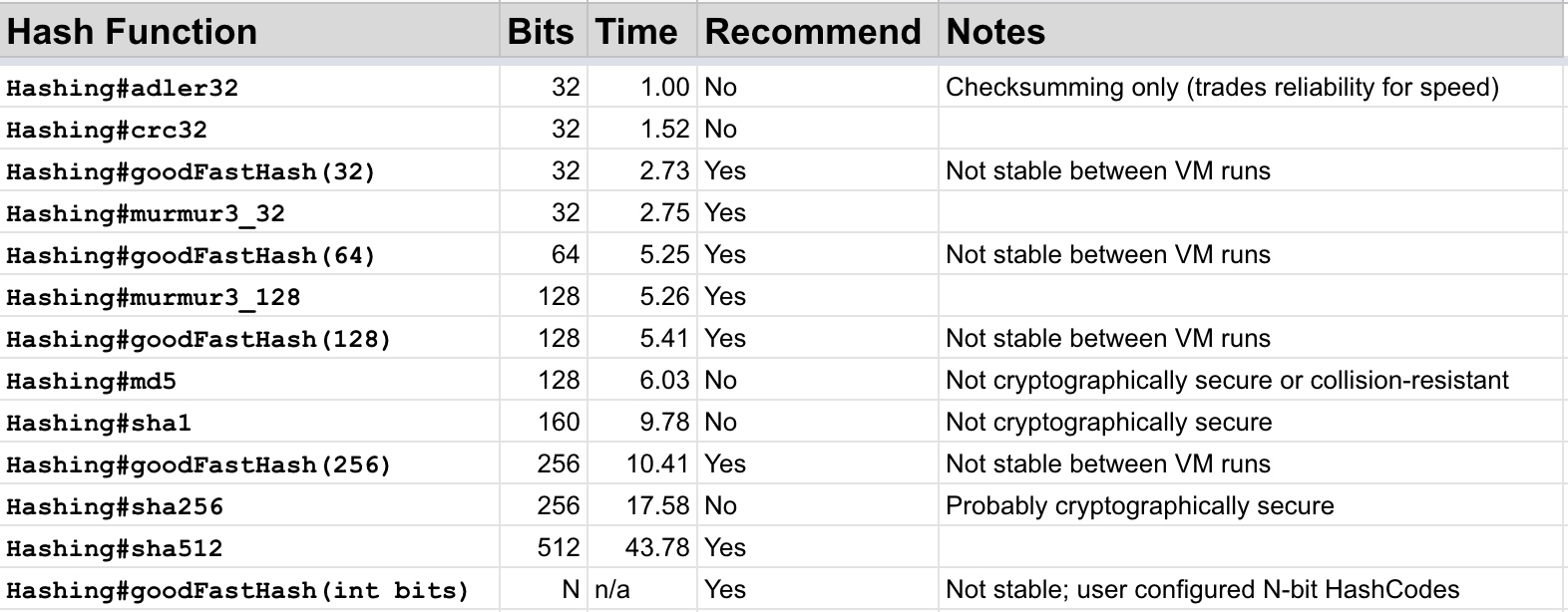
在负载均衡的场景下,哈希函数需要高性能、低碰撞率的特点,后来看到上图表格中的推荐实现中有两个murmur3的实现,于是就去搜索了一下,搜索完发现这个MurmurHash算法很不错,它是一种非密码学的哈希函数,相对来说性能比较好,安全性比较低,而且它还有碰撞率低的特点,正适合负载均衡这种场景;而且,在Jedis、Memcached、Cassandra等等这些项目中都使用的是它。MurmurHash发展到现在已经是第三版了,上图中实现的就是第三版的算法。
下面的代码是Jedis中MurmurHash的实现(我看的是Jedis 3.3.0的版本,实现的好像是MurmurHash2):
/**
* Hashes the bytes in a buffer from the current position to the limit.
* @param buf The bytes to hash.
* @param seed The seed for the hash.
* @return The 32 bit murmur hash of the bytes in the buffer.
*/
public static int hash(ByteBuffer buf, int seed) {
// save byte order for later restoration
ByteOrder byteOrder = buf.order();
buf.order(ByteOrder.LITTLE_ENDIAN);
int m = 0x5bd1e995;
int r = 24;
int h = seed ^ buf.remaining();
int k;
while (buf.remaining() >= 4) {
k = buf.getInt();
k *= m;
k ^= k >>> r;
k *= m;
h *= m;
h ^= k;
}
if (buf.remaining() > 0) {
ByteBuffer finish = ByteBuffer.allocate(4).order(ByteOrder.LITTLE_ENDIAN);
// for big-endian version, use this first:
// finish.position(4-buf.remaining());
finish.put(buf).rewind();
h ^= finish.getInt();
h *= m;
}
h ^= h >>> 13;
h *= m;
h ^= h >>> 15;
buf.order(byteOrder);
return h;
}
我会先用Jedis实现的MurmurHash2来实现解决问题的代码,分别以不加入虚拟节点、10个虚拟节点和20个虚拟节点来分别测试KV数据的分布情况和标准差。
后面可以加入其它的一致性哈希算法的实现来进行比较。
首先,声明一个哈希函数的接口:
public interface HashFunction {
/**
* Calculate input key's hash value.
*
* @param key key for calculated
* @return hash value
*/
long hash(String key);
}
我们只关注给定一个指定的key,返回哈希函数计算后的哈希值,所以只需要声明一个方法。
基于Jedis的MurmurHash2的实现:
public class MurmurHash2Function implements HashFunction {
/**
* Jedis's implement for MurmurHash2.
*
* @param key key for calculated
* @return hash value
*/
@Override
public long hash(String key) {
ByteBuffer buf = ByteBuffer.wrap(key.getBytes());
int seed = 0x1234ABCD;
ByteOrder byteOrder = buf.order();
buf.order(ByteOrder.LITTLE_ENDIAN);
long m = 0xc6a4a7935bd1e995L;
int r = 47;
long h = seed ^ (buf.remaining() * m);
long k;
while (buf.remaining() >= 8) {
k = buf.getLong();
k *= m;
k ^= k >>> r;
k *= m;
h ^= k;
h *= m;
}
if (buf.remaining() > 0) {
ByteBuffer finish = ByteBuffer.allocate(8).order(
ByteOrder.LITTLE_ENDIAN);
// for big-endian version, do this first:
// finish.position(8-buf.remaining());
finish.put(buf).rewind();
h ^= finish.getLong();
h *= m;
}
h ^= h >>> r;
h *= m;
h ^= h >>> r;
buf.order(byteOrder);
return h;
}
}
KV数据抽象为下面的接口:
public interface KvData<K,V> {
/**
* KV data's key, it can be use to do mapping operation with hash ring.
*
* @return kv data's key
*/
K key();
/**
* KV data's value.
* because we don't concern about this value in the question,
* so implement by default with return null value.
*
* @return kv data's value
*/
default V value() {
return null;
}
}
问题只需要知道KV数据的分布和分布数量的标准差,不需要关注KV数据的value,所以接口中直接以默认的value()方法实现。
题目中指定了是10台服务器,对于服务器节点,我们只需要关注它的唯一标识的key即可,所以抽象为如下接口:
public interface ServerNode {
/**
* Server node identify key for mapping to hash ring
*
* @return node key value
*/
String nodeKey();
}
核心的接口已经齐了,需要编码实现一致性哈希的映射类了,代码如下:
public class ConsistentHashMapper {
private final HashFunction hashFunction;
private final int virtualNodeNum;
private TreeMap<Long, ServerNode> hashRing = new TreeMap<>();
public ConsistentHashMapper(HashFunction hashFunction) {
this(hashFunction, 0);
}
public ConsistentHashMapper(HashFunction hashFunction, int virtualNodeNum) {
if (virtualNodeNum < 0 || virtualNodeNum > 1000) {
throw new IllegalArgumentException("virtual node number must between 0 and 1000");
}
this.hashFunction = hashFunction;
this.virtualNodeNum = virtualNodeNum;
}
/**
* Mapping kvData's key to hash ring,
* and return the mapped ServerNode.
*
* @param nodeList ServerNode list
* @param kvData KvData for mapping
* @return ServerNode mapped by kvData
*/
public ServerNode mapping(List<ServerNode> nodeList, KvData<String, Object> kvData) {
if (nodeList == null || nodeList.isEmpty()) {
throw new IllegalArgumentException("node list can not be null or empty");
}
if (kvData == null || kvData.key() == null || "".equals(kvData.key())) {
throw new IllegalArgumentException("kvData's hashKey is null or empty");
}
long hashValue = hashFunction.hash(kvData.key());
if (hashRing == null || hashRing.isEmpty()) {
hashRing = buildHashRing(nodeList);
}
return locate(hashRing, hashValue);
}
/**
* Addressing for hashValue in hash ring, return the first mapped ServerNode.
* if not mapped util to the end, return the first ServerNode in the hash ring.
*
* @param hashRing hash ring with mapped ServerNode list
* @param hashValue hash value need to addressing
* @return ServerNode
*/
private ServerNode locate(TreeMap<Long, ServerNode> hashRing, long hashValue) {
Map.Entry<Long, ServerNode> entry = hashRing.ceilingEntry(hashValue);
if (entry == null) {
entry = hashRing.firstEntry();
}
return entry.getValue();
}
/**
* Build the hash ring with input ServerNode list if hash ring not be built.
* If #{code virtualNodeNum} larger than zero, the hash ring will build with virtual nodes.
* The result is a TreeMap<Long, ServerNode>,
* the map key is ServerNode's #{code HashFunction.hash(ServerNode.nodeKey())},
* and the map value is ServerNode.
*
* @param nodeList ServerNode list
* @return ServerNode mapping info map
*/
private TreeMap<Long, ServerNode> buildHashRing(List<ServerNode> nodeList) {
TreeMap<Long, ServerNode> virtualNodeMap = new TreeMap<>();
// no virtual node number set, just add real node
if (virtualNodeNum <= 0) {
addRealNodes(virtualNodeMap, nodeList);
} else {
addVirtualNodes(virtualNodeMap, nodeList);
}
return virtualNodeMap;
}
private void addRealNodes(TreeMap<Long, ServerNode> virtualNodeMap, List<ServerNode> nodeList) {
for (ServerNode node : nodeList) {
virtualNodeMap.put(hashFunction.hash(node.nodeKey()), node);
}
}
private void addVirtualNodes(TreeMap<Long, ServerNode> virtualNodeMap, List<ServerNode> nodeList) {
for (ServerNode node : nodeList) {
for (int i = 0; i < virtualNodeNum; i++) {
// all mapped node is virtual node
virtualNodeMap.put(hashFunction.hash(node.nodeKey() + String.format("%03d", i)), node);
}
}
}
}
前面说了,我们会对每种哈希函数的实现进行多组测试,所以ConsistentHashMapper有一个virtualNodeNum属性,用于指定虚拟节点的数量,默认为0表示全部映射真实的节点。(我这里限定了一个virtualNodeNum值的范围为0~1000)
哈希函数和虚拟节点的数量是通过ConsistentHashMapper类的构造函数来指定的。
ConsistentHashMapper#mapper()方法接受两个参数:服务器节点的列表,以及要寻址的KV数据,返回的结果就是映射到的服务节点。
另外,需要计算标准差,所以增加了StatisticUtils类实现标准关的计算:
public class StatisticUtils {
/**
* Standard Deviation algorithm
*
* @param dataArr data array
* @return standard deviation result
*/
public static double stdev(Long[] dataArr){
double sum = 0.0;
double mean = 0.0;
double num = 0.0;
double numi = 0.0;
for (long i : dataArr) {
sum+=i;
}
mean = sum/dataArr.length;
for (long i : dataArr) {
numi = Math.pow(((double) i - mean), 2.0D);
num+=numi;
}
return Math.sqrt(num/dataArr.length);
}
}
剩下就是测试用例了:
public class TestConsistentHashMapper {
/**
* Mock ServerNode list
*/
private static final List<ServerNode> nodeList = Arrays.asList(
() -> newServerNodeKey("server01"),
() -> newServerNodeKey("server02"),
() -> newServerNodeKey("server03"),
() -> newServerNodeKey("server04"),
() -> newServerNodeKey("server05"),
() -> newServerNodeKey("server06"),
() -> newServerNodeKey("server07"),
() -> newServerNodeKey("server08"),
() -> newServerNodeKey("server09"),
() -> newServerNodeKey("server10")
);
private static String newServerNodeKey(String name) {
assertNotNull("server name can not be null", name);
return name;
}
private void initStatisticMap(List<ServerNode> nodeList, AtomicLongMap<String> statisticMap) {
for(ServerNode node : nodeList) {
statisticMap.put(node.nodeKey(), 0L);
}
}
//// test MurmurHash2 start ////
@Test
public void testMurmurHash2WithoutVirtualNode() {
System.out.println("MurmurHash2 with no virtual node: ");
ConsistentHashMapper hashMapper = new ConsistentHashMapper(new MurmurHash2Function());
process(hashMapper, AtomicLongMap.create());
}
@Test
public void testMurmurHash2With10VirtualNode() {
System.out.println("MurmurHash2 with 10 virtual node: ");
ConsistentHashMapper hashMapper = new ConsistentHashMapper(new MurmurHash2Function(), 10);
process(hashMapper, AtomicLongMap.create());
}
@Test
public void testMurmurHash2With30VirtualNode() {
System.out.println("MurmurHash2 with 30 virtual node: ");
ConsistentHashMapper hashMapper = new ConsistentHashMapper(new MurmurHash2Function(), 30);
process(hashMapper, AtomicLongMap.create());
}
@Test
public void testMurmurHash2With50VirtualNode() {
System.out.println("MurmurHash2 with 50 virtual node: ");
ConsistentHashMapper hashMapper = new ConsistentHashMapper(new MurmurHash2Function(), 50);
process(hashMapper, AtomicLongMap.create());
}
@Test
public void testMurmurHash2With80VirtualNode() {
System.out.println("MurmurHash2 with 80 virtual node: ");
ConsistentHashMapper hashMapper = new ConsistentHashMapper(new MurmurHash2Function(), 80);
process(hashMapper, AtomicLongMap.create());
}
@Test
public void testMurmurHash2With100VirtualNode() {
System.out.println("MurmurHash2 with 100 virtual node: ");
ConsistentHashMapper hashMapper = new ConsistentHashMapper(new MurmurHash2Function(), 100);
process(hashMapper, AtomicLongMap.create());
}
@Test
public void testMurmurHash2With200VirtualNode() {
System.out.println("MurmurHash2 with 200 virtual node: ");
ConsistentHashMapper hashMapper = new ConsistentHashMapper(new MurmurHash2Function(), 200);
process(hashMapper, AtomicLongMap.create());
}
@Test
public void testMurmurHash2With500VirtualNode() {
System.out.println("MurmurHash2 with 500 virtual node: ");
ConsistentHashMapper hashMapper = new ConsistentHashMapper(new MurmurHash2Function(), 500);
process(hashMapper, AtomicLongMap.create());
}
@Test
public void testMurmurHash2With800VirtualNode() {
System.out.println("MurmurHash2 with 800 virtual node: ");
ConsistentHashMapper hashMapper = new ConsistentHashMapper(new MurmurHash2Function(), 800);
process(hashMapper, AtomicLongMap.create());
}
@Test
public void testMurmurHash2With1000VirtualNode() {
System.out.println("MurmurHash2 with 1000 virtual node: ");
ConsistentHashMapper hashMapper = new ConsistentHashMapper(new MurmurHash2Function(), 1000);
process(hashMapper, AtomicLongMap.create());
}
//// test MurmurHash2 end ////
private void process(ConsistentHashMapper hashMapper, AtomicLongMap<String> statisticMap) {
initStatisticMap(nodeList, statisticMap);
processMappingWithLoop(hashMapper, statisticMap, 1000000);
prettyPrintStatisticMap(statisticMap);
}
private void processMappingWithLoop(ConsistentHashMapper hashMapper, AtomicLongMap<String> statisticMap, int timesOfLoop) {
for (int i = 0; i < timesOfLoop; i++) {
ServerNode node = hashMapper.mapping(nodeList, () -> UUID.randomUUID().toString().replaceAll("-", ""));
statisticMap.getAndIncrement(node.nodeKey());
}
}
private void prettyPrintStatisticMap(AtomicLongMap<String> statisticMap) {
statisticMap.asMap().entrySet().stream().sorted(Map.Entry.comparingByValue()).forEach(System.out::println);
System.out.print("Standard Deviation: ");
System.out.println(StatisticUtils.stdev(statisticMap.asMap().values().toArray(new Long[]{})));
System.out.println("\n");
}
}
输出结果如下:
MurmurHash2 with no virtual node:
server07=19330
server10=24227
server05=27170
server03=47946
server01=60284
server06=85404
server04=132435
server08=150064
server02=200011
server09=253129
Standard Deviation: 76852.16470601202
MurmurHash2 with 10 virtual node:
server06=46931
server01=61209
server10=70729
server08=77613
server02=78922
server04=97173
server09=110561
server05=121380
server03=151153
server07=184329
Standard Deviation: 40531.410579944044
MurmurHash2 with 30 virtual node:
server02=61015
server10=74404
server03=87075
server09=98883
server08=104283
server06=107033
server04=110190
server07=111261
server01=116286
server05=129570
Standard Deviation: 19445.72150885639
MurmurHash2 with 50 virtual node:
server10=78045
server05=84007
server03=86165
server08=95638
server02=96407
server09=99109
server01=108940
server07=111621
server04=119266
server06=120802
Standard Deviation: 14074.121905113654
MurmurHash2 with 80 virtual node:
server10=72738
server02=79641
server09=92611
server03=93406
server08=95787
server05=97055
server06=108303
server01=110413
server04=124253
server07=125793
Standard Deviation: 16471.37915294284
MurmurHash2 with 100 virtual node:
server10=79154
server02=88888
server08=90075
server03=95174
server05=98625
server06=103063
server09=103299
server04=109429
server01=110451
server07=121842
Standard Deviation: 11735.359227565214
MurmurHash2 with 200 virtual node:
server10=89203
server02=91204
server03=97569
server04=99208
server01=100367
server07=101756
server09=102103
server08=105518
server06=105586
server05=107486
Standard Deviation: 5708.017168859954
MurmurHash2 with 500 virtual node:
server10=93869
server02=94568
server05=97026
server04=98421
server09=99816
server07=101706
server03=101958
server08=104029
server01=104300
server06=104307
Standard Deviation: 3721.3552370070774
MurmurHash2 with 800 virtual node:
server02=92880
server05=95670
server07=98301
server06=98309
server08=99432
server01=100134
server10=100506
server04=101773
server03=104119
server09=108876
Standard Deviation: 4179.462453474131
MurmurHash2 with 1000 virtual node:
server02=95820
server05=96008
server01=97176
server08=97304
server06=100933
server10=100962
server07=101764
server04=102557
server03=102675
server09=104801
Standard Deviation: 3005.045091175838
上面的输出结果中,我把每组测试中,每个节点所映射到的KV的数量按从小到大的顺序进行了输出,这样可以方便看最大值与最小值之间的差距。
从由面的测试结果可以看出:增加虚拟节点可以有效的提升MurmurHash2实现的哈希函数的分布的均匀性。尤其是上面虚拟节点为1000时,10个节点的分布已经很均匀了(在+/-0.005之间)。
测试结果的标准差:
| test group | Standard Deviation |
|---|---|
| MurmurHash2 no virtual node | 76852.16470601202 |
| MurmurHash2 10 virtual node | 40531.410579944044 |
| MurmurHash2 30 virtual node | 19445.72150885639 |
| MurmurHash2 50 virtual node | 14074.121905113654 |
| MurmurHash2 80 virtual node | 16471.37915294284 |
| MurmurHash2 100 virtual node | 11735.359227565214 |
| MurmurHash2 200 virtual node | 5708.017168859954 |
| MurmurHash2 500 virtual node | 3721.3552370070774 |
| MurmurHash2 800 virtual node | 4179.462453474131 |
| MurmurHash2 1000 virtual node | 3005.045091175838 |
标准差的结果越低表示效果越好。下图为标准差的拆线图,横轴为节点数量,纵轴为标准差的值:
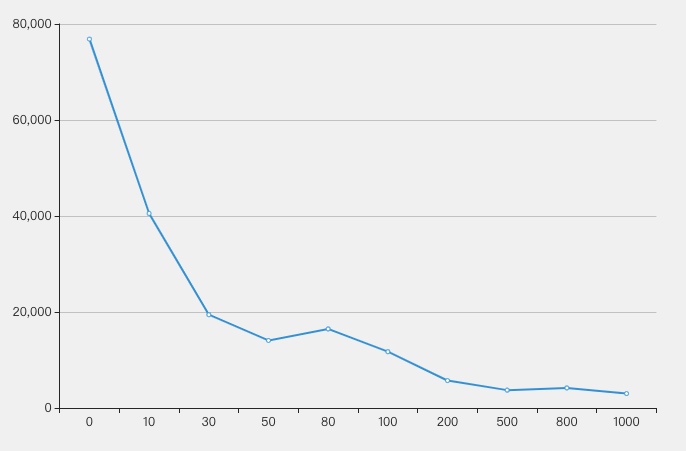
在示例代码中,还增加了Md5、sha256、MurmurHash3等不同的实现。
0x04 总结
本篇通过一道题目来深入了解了一致性哈希。
一致性哈希在分布式环境下使用非常广泛,不同的场景使用的哈希函数的实现也各不相同。对于一个哈希函数,我们主要关注以下几点:
- 算法的复杂度(时间、空间)
- 哈希值的分布均匀情况
- 哈希碰撞的概率
选择哈希函数,以及实现一致性哈希需要结合具体的业务场景。
比如,Guava中的Hashing#consistentHash()实现在减少桶(bucket)的数量后,会导致所有的映射发生偏移,在某些场景下是无法接受的。
再比如,上面的MurmurHash2Function实现中,现在是直接将结果(h)返回,但是,如果返回的h & 0xffffffffL,在增加虚拟节点的情况下,映射的分布要比直接返回结果均匀很多。
服务器节点的标识key、数据的key的设计与哈希函数的算法实现关系十分密切,虚拟节点的增加也能对映射的分布起到平衡的作用,但需要结合实际情况来测试虚拟节点的合适数值。
本文到此就结束了,代码在示例仓库中,示例代码中实现了多种不同的哈希函数实现,可以横向比较,其中也包括dubbo中的一致性哈希算法的实现,Guava中的MurmurHash3实现等等。
欢迎各交流与反馈!